Álgebra booleana. Parte 2. Leis e funções básicas

Continuação da história sobre álgebra booleana, convenções, regras, operações. Transição para o básico dos circuitos de contato.

Em primeiro artigo George Bull foi descrito como o criador da álgebra da lógica. O segundo artigo descreverá as operações básicas da álgebra booleana e métodos para simplificar expressões booleanas. Portanto, a álgebra booleana usa declarações como argumentos, e não seu significado, mas a verdade ou falsidade da declaração.

O formulário para escrever expressões na álgebra booleana.

Se a afirmação for verdadeira, está escrita assim: A = 1, se for falsa, então A = 0 (afinal, não é verdade que a batata é uma fruta). Para qualquer afirmação, A é verdadeiro (A = 1) ou falso (A = 0). Não pode haver meio aqui. Já falamos sobre isso.

Se você conectar duas instruções simples à união E, obterá uma declaração complexa, chamada de produto lógico. Vamos usar dois ditados simples: "Três são mais que dois", designaremos pela letra A, "Três menos que cinco" - pela letra B.

Portanto, a afirmação complexa “Três é mais que dois E menos que cinco” é lógica (neste caso, a letra maiúscula E diz que esta é uma operação lógica “E”, bem como posteriormente no texto “OU” e “NÃO”). e B. É designado da seguinte forma: A ^ B ou A * B.

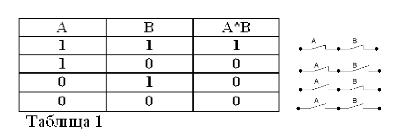
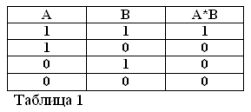
Multiplicação lógica (operação "AND").

Na álgebra elementar A * A = A2. Mas na álgebra de Buhl, A * A = A2 = A, A * A = A, já que o sinal de multiplicação (*) agora significa ... E ... no sentido de E ... E. Toda a nossa experiência confirma que A&A é a mesma que A. Somente não se pode discordar disso. A verdade da afirmação não muda se for repetida pelo fator várias vezes.

O produto de duas instruções é considerado verdadeiro (igual a 1), então, e somente se ambos os fatores forem verdadeiros e falso (igual a 0) se pelo menos um dos fatores for falso. Concorde que essas regras não contradizem o senso comum e, além disso, cumprem totalmente as regras da álgebra elementar:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

A primeira igualdade é a seguinte: se A e B forem verdadeiros, o produto A * B será verdadeiro. Na álgebra de Buhl, o sinal de multiplicação (*) substitui a união I.

Os produtos lógicos podem incluir não dois, mas um número maior de declarações - fatores. E, neste caso, o produto é verdadeiro apenas quando, ao mesmo tempo, todas as declarações-fatores são verdadeiras.

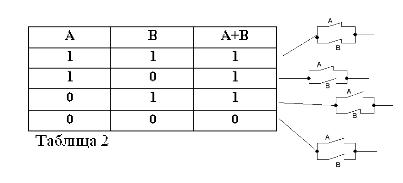
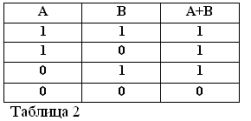
Adição lógica (operação OR)

Se duas instruções estiverem conectadas por uma união OU. essa frase composta formada é chamada de soma lógica.

Considere um exemplo de uma soma lógica. Dizendo A: "Hoje irei ao cinema".

Declaração B: "Hoje irei à discoteca". Adicionamos as duas afirmações e obtemos: "Hoje irei ao cinema OU a uma discoteca".

Essa declaração complexa é indicada da seguinte maneira: A + B = C ou (A V B) = C.

Por C, denotamos uma declaração complexa de uma soma lógica.

No exemplo em consideração, a união OR não pode ser usada em um sentido exclusivo. De fato, no mesmo dia você pode ir ao cinema e à discoteca. E aqui está o ditado:

“O presidente da parceria de jardinagem será Petrov ou Ivanov”, não é uma soma lógica, porque apenas uma pessoa será o presidente e a outra será um jardineiro comum amador.

O sinal V para a soma lógica é escolhido porque é a letra inicial da palavra latina "vel", que significa "ou", em contraste com a palavra latina "aut>, que significa" e ". Agora deve ficar claro para todos por que o produto lógico é indicado pelo sinal ^.

Na álgebra elementar existe uma regra A + A = 2A. Esta regra é verdadeira, não importa qual número seja representado pela letra A. Na álgebra booleana, a regra A + A = A. Corresponde a ela.Toda a nossa experiência de vida diz que dizer A ou A ou ambos A é apenas outra maneira mais longa de dizer apenas A.

Como qualquer declaração composta, a soma das duas declarações A e B pode ser verdadeira ou falsa. A soma é considerada verdadeira, ou seja, igual à unidade, se pelo menos um dos termos for verdadeiro:

A + B = 1 se OR A = 1 OR B = 1, o que é consistente com a aritmética convencional:

1+0 = 0+1 = 1.

Se ambas as afirmações somadas são verdadeiras, então a soma também é considerada verdadeira, portanto, na álgebra booleana, temos: (1) + (1) = 1.

Os colchetes são definidos aqui para enfatizar o condicional, o significado dessa adição e não a aritmética.

A soma de duas instruções é considerada falsa e igual a zero se, mas somente se os dois termos forem falsos. A partir daqui:

0 + 0=0.

Portanto, a soma das duas afirmações A + B é considerada verdadeira se verdadeira, OR A, OR B ou OR ambos os termos juntos. Assim, a palavra OR é denotada por +.

Lembrando que as afirmações A e B só podem ser verdadeiras ou falsas e, portanto, têm uma medida da verdade 1 ou 0, os resultados das operações AND e OR consideradas podem ser resumidos nas tabelas 1 e 2.

A terceira operação, amplamente utilizada pela álgebra de Buhl, é a operação de negação - NOT. Lembramos que a álgebra elementar usa as operações ADD, D Subtrair, Multiplicar por, Dividir por e outras.

Para cada afirmação A, há sua negação NÃO A, que iremos denotar pelo símbolo / A. Isso não deve estar em dúvida.

Damos exemplos: “Vamos para a floresta” A, “Não vamos para a floresta” / A.

Se a afirmação A é verdadeira, ou seja, A = 1, sua negação / A deve ser falsa / A = 0. E vice-versa, se alguma afirmação for falsa, sua negação é verdadeira. Por exemplo: “Um cavalo não come feno” / A = 0, “Um cavalo não come feno” (A = 1). Isso pode ser expresso na tabela 3.

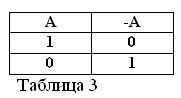
Determinando o significado da ação de negação e assumindo que uma das duas afirmações A e / A é sempre uma verdadeira, seguem duas novas fórmulas da álgebra booleana:

A + (/ A) = 1 e A * (/ A) = 0.

Também existem outras fórmulas que simplificam o processamento lógico de instruções. Por exemplo, 1 + A = 1, pois, de acordo com a definição de adição, no caso em que um termo é igual à unidade, a soma é sempre igual à unidade. O resultado obtido não depende de A = 0 ou A = 1.

Cada uma das três operações lógicas que examinamos (AND, OR, NOT) possui certas propriedades próximas das regras da álgebra elementar. Se todos eles forem formulados, obteremos 25 regras da álgebra booleana. Eles são suficientes para resolver quase qualquer problema lógico. Sem essas regras, torna-se bastante difícil resolver problemas lógicos devido à sua aparente complexidade. Tentar encontrar a resposta correta sem usar as regras significa substituí-las por engenhosidade e raciocínio geral. As regras facilitam muito esse trabalho e economizam tempo.

No âmbito do artigo, é impossível considerar todas essas 25 regras, mas aqueles que desejam podem sempre encontrá-las na literatura relevante.

Como já mencionado no primeiro artigo em 1938, o jovem cientista americano Claude Shannon em seu artigo "Análise simbólica de circuitos de relé e comutação" pela primeira vez usa álgebra booleana para problemas de tecnologia de relés. A descoberta de Shannon foi que ele percebeu que o método de projetar máquinas de retransmissão e computadores eletrônicos é na verdade um ramo da lógica matemática.

Isso acontece frequentemente. Por muitos anos, o cientista trabalha em um problema que parece completamente desnecessário para seus compatriotas - apenas divertido. Mas décadas e, às vezes, séculos se passam, e uma teoria de que ninguém precisa não apenas adquire o direito de existir, mas sem ela outros progressos se tornam impensáveis.

O que ajudou Shannon a "descobrir" a álgebra booleana pela segunda vez? Case? Nada disso.

O amor pelas máquinas de retransmissão, construídas com interruptores e retransmissores convencionais, ajudou o jovem cientista a conectar uma teoria esquecida às tarefas de trocas telefônicas automáticas, nas quais trabalhava na época. Mais tarde, Shannon introduziu a mesma idéia de "sim ou não" em mensagens discretas e lançou as bases para uma seção inteira da cibernética - a teoria da informação.

A álgebra de Buhl era muito adequada para a análise e síntese de circuitos de relé. Foi o suficiente para aceitar como uma afirmação verdadeira: “Há um sinal no circuito” e, como falsa - “Não há sinal no circuito”, como uma nova álgebra apareceu - a álgebra do sinal, a álgebra do circuito de relé.

A nova álgebra é válida apenas para a consideração de relés e circuitos de comutação. Afinal, somente nesses esquemas a condição "existe um sinal" e "nenhum sinal" é satisfeita. Onde o sinal muda continuamente, adquirindo um número arbitrariamente grande de condições intermediárias (esse sinal é chamado analógico), a álgebra de relé não é aplicável. Isso sempre deve ser lembrado. Mas apenas a maioria dos computadores eletrônicos e máquinas cibernéticas usa o princípio discreto do processamento de sinais, que se baseia nos elementos "sim - não".

A expressão “Contato fechado” foi aceita por Shannon como verdadeira (1) e “Contato aberto” como falsa (0). O resto da "álgebra", incluindo as operações AND, OR e NOT e 25 regras, Shannon pediu emprestado a Boole.

A álgebra do circuito de relé acabou sendo mais simples que a álgebra booleana, uma vez que lida apenas com elementos do tipo "sim - não". Além disso, a nova álgebra é mais visual.

Os elementos nesta álgebra são os contatos, que indicaremos pelas letras A, B, C ... O contato está fechado - A, o contato está aberto - / A (letra com um traço).

A notação, como você vê, é completamente retirada da álgebra booleana. Um contato aberto é uma negação de um contato fechado. O mesmo contato não pode ser fechado e aberto.

Vamos concordar que, se em qualquer circuito dois contatos forem indicados pela mesma letra, isso significa que eles sempre terão os mesmos valores.

A qualquer momento, ambos estão abertos ao mesmo tempo ou ambos estão fechados. A maneira mais fácil de imaginá-los conectados mecanicamente, para que ambos abram ou fechem simultaneamente.

Se em alguma cadeia um contato é uma negação de outro contato, então seus significados são sempre opostos. Por exemplo, os contatos C e / C nunca podem ser abertos simultaneamente ou fechados simultaneamente. E no diagrama, eles podem ser representados mecanicamente conectados: se um deles se abre, o outro se fecha.

Começamos a conhecer a álgebra de relé analisando os circuitos mais simples correspondentes às operações AND, OR e NOT.

O produto de dois contatos (operação AND) é o circuito obtido como resultado da conexão em série: ele é fechado (igual a 1) somente quando os dois contatos estão fechados (igual a 1).

A soma de dois contatos (operação OR) será o circuito formado quando eles estiverem conectados em paralelo: ele será fechado (igual a 1) quando pelo menos um dos contatos que formam o circuito estiver fechado (igual a 1).

O oposto deste contato (operação NÃO) é um contato igual a 0 (aberto) se esse contato for 1 (fechado) e vice-versa.

Como na álgebra booleana, se os contatos forem indicados pelas letras A e B, denotaremos o produto de dois contatos por A * B, a soma por A + B e o contato oposto A, por / A. O exposto acima é explicado nas Figuras 1, 2 e 3.

Validade das tabelas correspondentes às operações AND, OR e NOT. agora ninguém deveria estar em dúvida.

Vamos nos debruçar sobre dois exemplos: 1 * 0 = 0 e 1 + 0 = 1.

Pode ser visto na figura que um contato permanentemente fechado conectado em série com um contato permanentemente aberto é equivalente a um contato permanentemente aberto (1 * 0 = 0) Um contato permanentemente fechado conectado em paralelo com um contato permanentemente aberto é equivalente a um contato permanentemente fechado.

Tendo se familiarizado com a aritmética dos circuitos de contato, você pode descrever qualquer circuito de relé com uma fórmula usando as convenções aceitas. Na cibernética, essas fórmulas são chamadas estruturais.

Se a fórmula estrutural de qualquer circuito de relé for 1, um sinal poderá passar por ele - o circuito está fechado. Por outro lado, se a fórmula estrutural do circuito for 0, o sinal não passará por ele - o circuito está quebrado.Conclusão: dois circuitos de relé são equivalentes entre si quando suas fórmulas estruturais são iguais.

Na continuação do artigo, consideraremos exemplos de circuitos de contato, circuitos de contato típicos e seus equivalentes, além de elaborar diagramas de acordo com fórmulas estruturais. Também consideramos os principais circuitos lógicos que executam as funções da álgebra booleana.

Continuação do artigo: Álgebra booleana. Parte 3. Esquemas de contato

Boris Aladyshkin